1. Probabilidade

A Teoria da Probabilidade desenvolve modelos para tratar de experimentos
que quando são repetidos, geralmente, produzem resultados diferentes.
Esses são chamados de experimentos aleatórios ou fenômenos aleatórios.

Dado um experimento aleatório, diz-se que seu espaço amostral
$\Omega$ é o conjunto formado por todos os resultados possíveis do
experimento aleatório. Em uma definição menos formal dada por Jerônimo
Cardano (1501-1576), a probabilidade é definida como o quociente do
‘número de casos favoráveis’ sobre o ‘número de casos possíveis’:

\begin{equation}
P=\frac{\#\quad casos\quad favor\acute{a}veis}{\#\quad casos\quad poss\acute{\imath}veis}
\end{equation}

Cada elemento do espaço amostral é chamado deevento
elementar e, os subconjuntos de $\Omega$ são chamados de eventos.
Assim, uma noção mais geral de probabilidade é dada pela seguinte
definição:

Uma função $P$ cujo seu domínio é o espaço amostral $\varOmega$
definida sobre todos os eventos de $\varOmega$(subconjuntos $A$)
é chamada de probabilidade se:

1. $1\leq P(A)\leq1$, $\forall A\subset\varOmega$ ;
2. $P(\oslash)=0$ (pois $\#\oslash=0$), $P(\varOmega)=1$;
3. Se $A$ e $B$ são eventos disjuntos$(A\cap B=\oslash)$, então $P(A\cup B)=P(A)+P(B)$.

Várias consequências úteis seguem da definição anterior, das quais
destacamos algumas proposições:

1. Probabilidade Complementar: $P(A^{c})=1-P(A)$;
2. Se $A\subset B$ então $P(A)=P(B)-P(B-A)$;
3. Se $A\cap B\neq\oslash$, então, $P(A\cup B)=P(A)+P(B)-P(A\cap B)$;

Para ilustrar a aplicação das definições e proposições listadas segue
o exemplo: Um número entre 1 a 50 é escolhido aleatoriamente. Qual
a probabilidade que ele seja divisível por 5 ou par.

Portanto,

$P(div5)=$$\frac{10}{50}=\frac{1}{5}$;$P(par)=\frac{25}{50}=\frac{1}{2}$
; $P(div5\cap par)=\frac{5}{50}=\frac{1}{10}$. Utilizando a proposição
$(P3)$ temos,

$P(div5\cup par)=P(div5)+P(par)-P(div5\cap par)=\frac{1}{5}+\frac{1}{2}-\frac{1}{10}=\frac{2+5-1}{10}=\frac{6}{10}=0,6$.

2. Variável aleatória discreta

Quando o espaço amostral $\varOmega$ de um experimento não é constituído
por número reais, como por exemplo, o lançamento de uma moeda $\varOmega=\{CARA,COROA\}$,
as técnicas da Estatística Descritiva não podem ser aplicadas diretamente.
Para que essas ferramentas possam ser utilizadas é necessário estabelecer
uma função que transforme o espaço amostral não numérico em um espaço
amostral numérico. Este é o objetivo de se definir uma variável
aleatória(VA). Ainda no caso do lançamento da moeda, se denotarmos
a variável aleatória $x$ como sendo $1$ para o resultado do lançamento
CARA e $0$ para o caso que a face da moeda observada após o lançamento
seja COROA, nota-se que a variável aleatória $x$ transformou o espaço
amostral $\{CARA,COROA\}$ para $\{0,1\}$.

Uma outra forma de analisar a situação segue da definição: Associa-se
um conjunto de valores para uma característica (observável) de uma
coleção de indivíduos (população) de interesse . Como consequência,
segue de $(1)$ que $P(x=1)=P(x=0)=1/2$. Onde $P(x)$ é a função
de probabilidade associada a variável aleatória $x$.

Para se estudar a distribuição de frequências $f_{i}$ de uma sequência
de VA’s $x_{1},x_{2},x_{3},…,x_{n}$ independentes (ex. vários lançamentos
de uma moeda), ou seja, a estatística da amostra $x_{1},x_{2},x_{3},…,x_{n}$,
procura-se caracterizar algumas medidas da distribuição.

Grandezas úteis :

(i) Valor Esperado:

\begin{equation}
E(x)=\sum x_{i}P(x_{i})
\end{equation}

(ii) Média:

\begin{equation}
<x> = \frac{1}{n}(x_{1}+x_{2}+x_{3}+…,+x_{n})=\frac{\sum x_{i}f_{i}}{\sum f_{i}}=\frac{\sum x_{i}f_{i}}{n}
\end{equation}

A variância pode ser calculada de modo mais rápido pela simplificação:

\begin{equation}
\sigma^{2}(x)=E(x^{2})-[E(x)]^{2}
\end{equation}

(iv) Desvio Padrão:

\begin{equation}
d(x)=\sqrt{\sigma^{2}(x)}
\end{equation}

(v) Erro Padrão:

\begin{equation}
SE=\frac{d(x)}{\sqrt{n}}
\end{equation}

~

a. Qual a diferença entre valor esperado e média ?

b. No lançamento de dois dados de quatro lados que possuem valores
de 1 a 4 em suas faces, a variável aleatória $x$ anota a soma dos
pontos da face superior. Determine a média, a variância e o desvio-padrão
da variável aleatória $x$. Esboce o gráfico de $P(x)$.

3. Variável aleatória contínua:

Grandezas úteis :

(i) Densidade de probabilidade:

$\rho(x)\geq0$ e $\int_{-\infty}^{\infty}\rho(x)dx=1$.

(ii) Média:

$<x>=\int x\rho(x)dx$

(iii) Distribuição acumulada:

$F(x)=\int_{-\infty}^{x}\rho(y)dy$

(iv) Distribuição acumulada complementar: probabilidade de um valor
ser maior ou igual a $x$.

$F'(x)=\int_{x}^{\infty}\rho(y)dy$

~

c. Dada a variável aleatória $x$ com densidade de probabilidade constante
$\frac{1}{b-a}$ onde $x\epsilon[a,b].$ Se $y=K+x$, calcule $$
para $K$ constante.

d. Alguns modelos em econofísica propõe que distribuição de renda
$m$ de uma dada população seja dividida em duas classes: os mais
ricos seguiriam uma distribuição do tipo Pareto e, o resto da população
uma distribuição do tipo Gibbs-Boltzmann como pode ser visto na figura
a seguir:

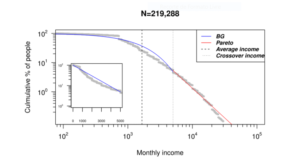
De forma geral escrevemos:

$P(m)=\frac{1}{T}\theta(m_{l}-m)\exp(-m/T)+\frac{A\theta(m-m_{l})}{m^{(1+\alpha)}}$

onde $T$ representa a renda média $,$ $m_{l}$ o valor de corte
entre as distribuções, $\alpha$ é conhecido como expoente de Pareto
e $A$ é simplesmente uma constante.

d.1. Reconhecendo que na grande maioria dos casos $\alpha\sim1.5$
e que $\frac{m_{l}}{T}\gg1$, obtenha a expressão para distribuição
acumulada complementar da variável aleatória $m$ e interprete seu
resultado.

d.2. Se 5\% da população segue a distribuição de Pareto (mais ricos)
e a renda média da população é de $1650R\$$ obtenha para essa situação
o valor de $m_{l}$.

4. Momentos de uma distribuição:

$\mu_{n}=<x^{n}>=\int x^{n}\rho(x)dx$</x^{n}>

onde:

$\mu_{1}=$ e $\mu_{2}-\mu_{1}^{2}=$$\sigma^{2}(x)$.

~

e. Derive para a distribuição Gaussiana uma regra geral para seus
momentos.

5. Função característica:

Calculada a partir da transformada de Fourier (discreta/ contínua)
da variável aleatória $x$.

$G(k)=\int\rho(x)exp(ikx)dx=<exp(ikx)>$

~

f. Derive a aproximação $g(k)=1+\sum_{n=1}^{\infty}$$\frac{(ik)^{n}}{n!}\mu_{n}$
( Se $g(k)$ não possuí desenvolvimento em série de Taylor, então,
$\rho(x)$ não possuí momentos).

g. Tome o logaritmo da expressão anterior redefinindo $ln(g(k))=\sum\frac{(ik)^{n}}{n!}\kappa_{n}$,
onde $\kappa_{n}$ são os cumulantes da distribuição. Após, encontre
as relações entre os cumulantes e momentos para $n=1,2$.

h. Calcule a função característica para a distribuição de probabilidade
Lorentziana.

6. Mudança de Variável:

Se $x$ e $y$ são variáveis aleatórias onde $y=f(x)$ e $\rho(x)$
é a densidade de probabilidade associada a $x$, então:

$\varrho(y)=\int\delta(y-f(x))\rho(x)dx$

e para intervalos infinitesimais:

$\varrho(y)=\sum_{n}\rho(x^{n})\shortmid\frac{dx^{n}}{dy}\shortmid$
, onde $n$ representa o número de intervalos infinitesimais da VA
$x$ que se mapeiam no intervalo $\triangle y$ de interesse.

i. Se $y=x^{2}-1$ e $\rho(x)=\lambda exp(-\lambda x)$ obtenha a
densidade de probabilidade $\rho(y)$ verificando a equivalência entre
as 2 maneiras propostas para a realização da mudança de variável.

7. Distribuição conjunta:

a densidade conjunta deve respeitar as seguintes condições:

$\int\rho(x,y)dxdy=1$ e $\rho(x,y)\geq0$

a partir delas pode-se obter as densidades marginais:

$\rho_{1}(x)=\int\rho(x,y)dy$; $\rho_{2}(y)=\int\rho(x,y)dx$;

Se $\rho(x,y)=\rho_{1}(x)\rho_{2}(y)$ então $=$ o que
significa dizer que não há correlação entre as variáveis.

~

j. Dada a distribuição de velocidades de Maxwell $\rho(x,y,z)=(\frac{\beta m}{2\pi})^{3/2}exp(-\beta m(v_{x}^{2}+v_{y}^{2}+v_{z}^{2})/2)$
a partir da relação $\rho_{e}(E)dE=\rho_{v}(v)dv$ calcule $\rho_{e}(E)$.